
Hollow sphere of radius r and mass m with axis of rotation going through its center. Rod of length L and mass m with two axes of rotation: about its center and one end.

Solid right circular cone of radius r, height h, and mass m with three axes of rotation passing through its center: parallel to the x, y, or z axes. Hollow right circular cone of radius r, height h, and mass m with three axes of rotation passing through its center: parallel to the x, y, or z axes. Plane regular polygon with n vertices, radius of the circumscribed circle R, and mass m with axis of rotation passing through its center, perpendicular to the plane. Thin rectangular plate of length l, width w, and mass m with axis of rotation going through its center, perpendicular to the plane. Point mass m at a distance r from the axis of rotation. Solid and hollow, regular octahedron (eight flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. An isosceles triangle of mass m, vertex angle 2β, and common-side length L with axis of rotation through tip, perpendicular to plane. Solid and hollow, regular icosahedron (twenty flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. Solid ellipsoid of semiaxes a, b, c, and mass m with three axes of rotation going through its center: parallel to the a, b, or c semiaxes.
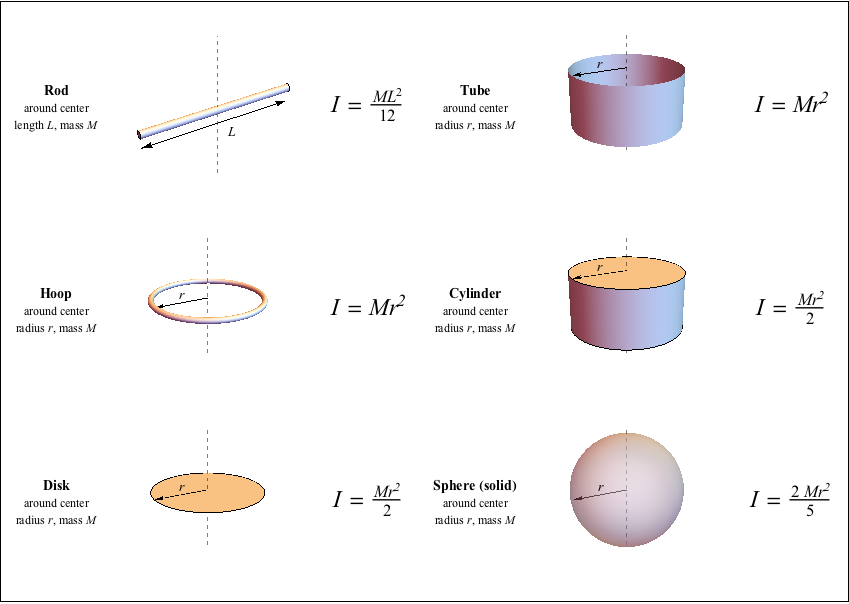
Solid and hollow, regular dodecahedron (twelve flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. Thin solid disk of radius r and mass m with three axes of rotation going through its center: parallel to the x, y or z axes. Cylindrical shell of radius r and mass m with axis of rotation going through its center, parallel to the height. Cylindrical tube of inner radius r₁, outer radius r₂, height h and mass m with three axes of rotation going through its center: parallel to x, y and z axes. Solid cylinder of radius r, height h and mass m with three axes of rotation going through its center: parallel to x, y and z axes. Solid cuboid of length l, width w, height h and mass m with four axes of rotation going through its center: parallel to the length l, width w, height h or to the longest diagonal d. Thin circular hoop of radius r and mass m with three axes of rotation going through its center: parallel to the x, y or z axes. Solid ball of radius r and mass m with axis of rotation going through its center. The other formulas provided are usually more useful and represent the most common situations that physicists run into.#1 - Ball. This formula is the most "brute force" approach to calculating the moment of inertia. A new axis of rotation ends up with a different formula, even if the physical shape of the object remains the same. The consequence of this formula is that the same object gets a different moment of inertia value, depending on how it is rotating. You do this for all of the particles that make up the rotating object and then add those values together, and that gives the moment of inertia. Basically, for any rotating object, the moment of inertia can be calculated by taking the distance of each particle from the axis of rotation ( r in the equation), squaring that value (that's the r 2 term), and multiplying it times the mass of that particle. The general formula represents the most basic conceptual understanding of the moment of inertia.

The general formula for deriving the moment of inertia.


 0 kommentar(er)
0 kommentar(er)
